بررسی پرسش 77 آزمون ورودی دهم: دبیرستان‌های استعدادهای درخشان: سال تحصیلی 96-97

دو شش ضلعی منتظم با طول ضلع و یک پنج ضلعی منتظم با طول ضلع را به چند طریق مختلف می‌توان از اضلاع به هم چسباند، به طوری که با دوران یا تقارن به هم تبدیل نشوند؟

1) 3
2) 4
3)
4) 9

ابهام: در صورت پرسش به روشنی تصریح نشده است که دو چند ضلعی می‌توانند چنان به هم چسبیده شوند، که سطح آن‌ها هم‌پوشانی داشته باشد یا نه. بنابراین باید برای یافتن پاسخ هر دو حالت را بررسی کرد.

• حالت نخست: هم‌پوشانی مجاز نیست.

در هر صورت پنج ضلعی منتظم باید از یک ضلع خود به یکی از شش ضلعی‌ها بچسبد (شکل الف).

چنان که در شکل الف می‌بینید، شش ضلعی دوم ممکن است به هر یک از ضلع‌های a یا یا c یا یا e یا یا ‎b'‎ یا یا ‎d'‎ بچسبد.

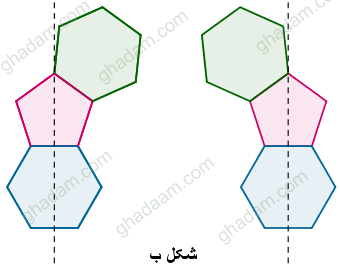
اما جفت ضلع‌های ‎(a , a')‎ و ‎(b , b')‎ و ‎(c , )‎ و ‎(d , d')‎ نسبت به عمود منطف ضلع e متقارن هستند،‌ پس اگر شش ضلعی دوم به ضلع a یا ‎a'‎ بچسبد، دو شکل به دست می‌آید که نسبت به عمود منصف ضلع e قرینه‌اند و با تقارن نسبت به همین عمود منصف به یکدیگر تبدیل می‌شوند (شکل ب).

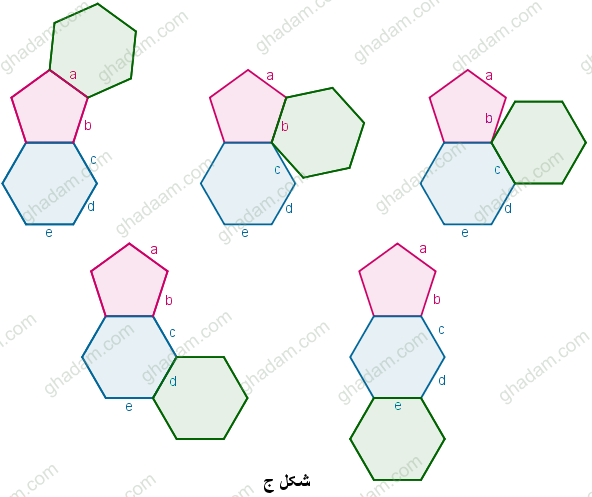
بنابراین در حالتی که شکل‌ها اجازه‌ی هم‌پوشانی نداشته باشند، تنها ترکیب مختلف از به هم چسبیدن این سه چند ضلعی به دست می‌آید. که نتیجه‌ی چسباندن شش ضلعی دوم به هر یک از ضلع‌های a یا یا c یا e از شکل الف هستند.
ببینید:

• حالت دوم: هم‌پوشانی مجاز است.

در هر صورت پنج ضلعی منتظم باید از یک ضلع خود به یکی از شش ضلعی‌ها بچسبد.

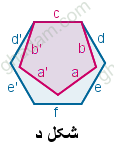
شکل د نیز نسبت به عمود منصف f متقارن است.
پس مثلا چسبیدن شش ضلعی منتظم دوم به ضلع‌های d و ‎d'‎ دو ترکیب به دست می‌دهد که با تقارن به هم تبدیل می‌شوند:

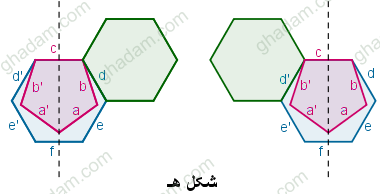
بنابراین چسباندن شش ضلعی منتظم دوم به هر یک از جفت ضلع‌های ‎(a , )‎ و ‎(b , b')‎ و ‎(d , d')‎ و ‎(e , e')‎ جفت شکل‌هایی مشابه شکل هـ به دست می‌دهند که با تقارن به هم تبدیل می‌شوند.

بنابراین در حالتی که شکل‌ها اجازه‌ی هم‌پوشانی داشته باشند، 6 ترکیب جدید و مختلف از به هم چسبیدن این سه چند ضلعی به دست می‌آید. که نتیجه‌ی چسباندن شش ضلعی دوم به هر یک از ضلع‌های a یا b یا یا d یا e یا از شکل د هستند.
امّا نباید از یاد ببریم که در هر یک از این شش حالت شش ضلعی منتظم دوم دو جور می‌تواند به ضلع یاد شده بچسبد. یک جور بدون هم پوشانی و یک جور با هم پوشانی. اگر بخواهیم شش ضلعی دوم را با هم پوشانی به ضلع شش ضلعی اوّل بچسبانیم، حالتی پیش می‌آید که پایین‌تر به آن توجّه کرده‌ایم. و در همه‌ی حالت‌ها به یک شکل می‌رسیم. امّا اگر شش ضلعی دوم را به ضلع پنج ضلعی بچسبانیم، حالت هم پوشانی و حالت بدون هم پوشانی شکل‌های متمایزی را می‌سازند. دو ترکیب پایانی در شکل زیر مربوط به حالت هم پوشانی است. ببینید:

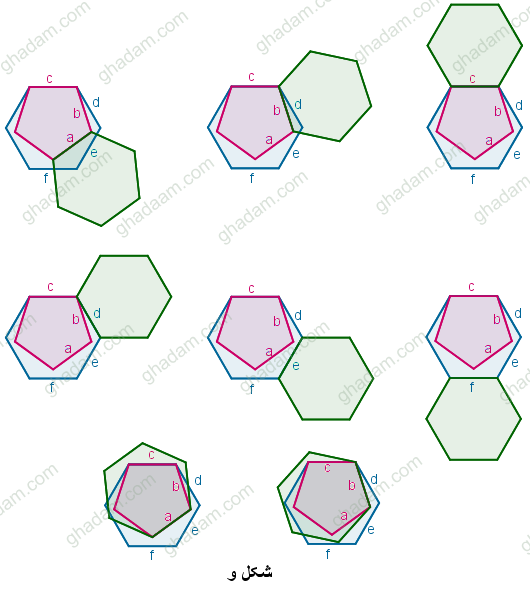
در حالتی که هم‌پوشانی مجاز باشد، حالت ویژه‌ای هست که نباید فراموش شود. ممکن است دو چند ضلعی پس از چسبیدن به هم، کاملا بر هم منطبق شوند. چنین چیزی برای پنج ضلعی منتظم و شش ضلعی منتظم شدنی نیست. ولی برای دو شش ضلعی منتظم شدنی است. پس در هر یک از ترکیب‌های شکل و که دو شش ضلعی با هم هم‌پوشانی ندارند، شش ضلعی دوم می‌توانست کاملا بر شش ضلعی اول منطبق شود. که در این صورت فرقی ندارد ضلع مشترک را c یا d یا e یا f یا ... بگیریم و در همه‌ی این حالت‌ها تنها به دو شکل می رسیم. یکی برای وقتی که پنج ضلعی منتظم درون دو شش ضلعی منتظم باشد و دیگری برای وقتی که پنج ضلعی منتظم بیرون شش ضلعی منتظم باشد.
ببینید:

اگر هم‌پوشانی مجاز نباشد، تنها ترکیب‌های شکل ج را باید بشماریم که تا هستند.

اگر هم‌پوشانی مجاز باشد، ترکیب شکل ج، ترکیب شکل و به علاوه‌ی ترکیب از شکل ز باید شمرده شوند. یعنی در این صورت 15 حالت مختلف داریم.

پس به نظر می‌رسد که منظور پرسش آزمون شمردن ترکیب‌هایی است که هم‌پوشانی ندارند. زیرا در گزینه‌ها عدد 15 نیست. ولی عدد 5 هست.