داستان‌های ریاضی – استدلال 1

گویی زبان یکسان نداریم. دانش‌آموز چیزی می‌گوید و من چیز دیگری. نگاهش می‌کنم و آرزو می‌کنم بتوانم یادش بدهم که استدلال کند و از چشمانش می‌خوانم که او هم آرزو دارد من حرف او را بفهمم. درگیری ساده‌ای است. هر دو پذیرفته‌ایم که دو پاره خطّ ‌و AQ هم طول هستند. امّا من استدلال مفصّلی دارم و او بسیار ساده و روان استدلال می‌کند. از شما چه پنهان بیش‌تر بچّه‌های کلاس با او همراه و هم سخن اند و همگی شگفت زده شده‌اند و می‌گویند ” آقا، چرا این‌قدر مطلب را می‌پیچانی؟ چیز به این سادگی این قدر دنگ و فنگ ندارد! “

گویا حوصله دارید و تا اینجا را خوانده‌اید. پس بد نیست شما را هم به وسط گفتگو و درگیری ببرم.

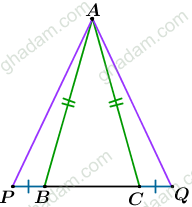مثلّث ABC در راس متساوی‌السّاقین است. دو نقطه‌ی متمایز P و Q را روی امتداد (و نه روی BC) جوری گرفته‌ایم که B بین C و باشد و ‎PB=CQ‎ باشد. ثابت کنید ‎AP=AQ‎ است.

استدلال من

داده (فرض): ‎AB=AC‎ , ‎PB=CQ‎, و به ترتیب روی امتداد BC از سوی B و C هستند.
حکم (خواسته): ‎AP=AQ‎

‎ΔABC: AB = AC‎ (بنا بر فرض) ‎_^قضیه__> ∠ABC=∠ACB‎

-> - ∠ABC = 180˚ - ∠ACB -> ∠ABP=∠ACQ (1)

‎ = AC‎ بنا بر فرض ‎(2)

‎ = CQ‎ بنا بر فرض ‎(3)

(1) , (2) , (3) _^ض‌زض__> ΔABP≅ΔACQ(4)

(1), (4) _^{اجزای نظیر}__>

امّا استدلال ساده و روان مرتضی:

چون ضلع BC را از دو طرف به یک اندازه امتداد داده‌ایم (چون ‎BP=CQ‎ داده‌ی مساله است، حرف ما نیست.) وقتی و Q را به A وصل می‌کنیم، پاره خط‌های برابر AP و پدیدار می‌شوند.

مرتضی و دیگر دوستانش به همین سادگی کار را به پایان رسانده‌اند و چشم به راه امتیاز زیبایی فن هستند. (گاهی داوران به کشتی گیری که یک فن را به زیبایی بسیار اجرا کند،‌ امتیاز اضافه‌تری بابت زیبایی اجرای فن می‌دهند.) امّا هنگامی که من گفتم استدلالشان نادرست است، با چشم‌های گرد و بُراق نگاهم کردند و پس از کمی سکوت، بهرام که همیشه سنجیده‌تر سخن می‌گفت از من خواست که نادرستی استدلال را با یک مثال نقض نشان بدهم: “آقا اگر راست می‌گویید، یک مورد بیاورید که نشان بدهد استدلال ما درست نیست.” همه پذیرفتند و من نیز!

گفتم: بچّه‌ها پیش از بیان مثالم، تأکید می‌کنم که برابری ‎AP=AQ‎ درست است. امّا از استدلال شما نتیجه نمی‌شود. استدلال شما برای اثبات این برابری بسیار نارسا و بریده، و از همه بیش‌تر گنگ و گرد است.

مثال من برای نارسایی استدلال مرتضی:

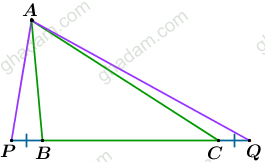مثلّث دلخواه ABC را کشیدم و ضلع BC را از دو طرف به یک اندازه تا و Q امتداد دادم و P و Q را به وصل کردم.

داد مرتضی در آمد که ”همه‌ی حرف من در باره‌ی مثلّث متساوی السّاقین بود. حرف مرا کج کرده‌اید. من چنان حرفی را چنین جایی نگفتم.”
من: اگر گفتم که استدلالت گنگ و گرد است، همین را منظور داشتم. بار دیگر به استدلالت نگاه کن. کجای استدلالت گفته‌ای که در باره‌ی مثلّث متساوی السّاقین صحبت می‌کنی؟ هیچ جا! و بعد ادّعا می‌کنی که استدلالت کارا و کارگر است. من هم استدلالت را در باره‌ی مثلّث دلخواه ABC‌ به کار بردم و دیدیم که به بیراهه رفت.

مرتضی: قبول کنید که ملّا نقطی هستید. ولی باشد. این که کاری ندارد. من هم دقیق‌تر استدلال می‌کنم. ببینید:

در مثلّث متساوی السّاقین ABC، چون ضلع BC را از دو طرف به یک اندازه امتداد داده‌ایم (چون BP=CQ داده‌ی مساله است و حرف ما نیست.) تا P و Q به دست آمده‌اند. (هنگام این اصلاح، مرتضی نگاه ویژه‌ای داشت.) وقتی و Q را به A وصل می‌کنیم، پاره خط‌های برابر AP و AQ پدیدار می‌شوند.
من: مرتضی و دیگران. خوب حواستان را جمع کنید. اگر اصلاح دیگری دارید، بگویید. چون هنوز گنگ و گرد سخن گفته‌اید.
بهرام: آقا گمانم دارید ما را آزمایش می‌کنید. خیالتان راحت باشد. اکنون استدلال ما کامل و تمام است. اگر نیست، بگویید.

مثال من برای نارسایی استدلال دوم:

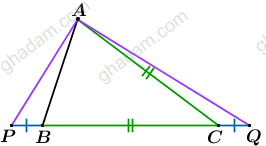مثلّث ABC ‌در راس ‌ متساوی‌السّاقین است. ساق BC را از دو طرف به یک اندازه امتداد می‌دهیم تا نقطه‌های P و Q به دست آیند. آیا AP و هم طول‌اند؟

بهرام و مرتضی و چند نفر دیگر ساکت بودند. می‌دانستم به چه می‌اندیشند. ولی چند نفری، هنوز حق را نزد خود می‌دیدند.
سعید: آقا همه‌ی ما از طرز صحبت مرتضی و بهرام فهمیدیم که دارند قاعده‌ی مثلّث متساوی‌السّاقین را امتداد می‌دهند، نه ساق را. امّا شما دارید لج می‌کنید.

من: به جای خوبی رسیدیم. کمی به استدلال من نگاه کنید. لحن ندارد. چیزی کم و کاست ندارد. یکی از تفاوت‌های بسیار گرامی استدلال و سخنان دیگر همین است. استدلال لحن ندارد. بسیار گویا است. گنگ و گرد نیست. استدلال پیامی بسیار روشن را بی هیچ پرده و کنایه‌ای نشان می‌دهد.

از طرفی از همه‌ی شما بچّه‌ها می‌خواهم به سکوت مرتضی و بهرام بنگرید. دارند آماده می‌شوند. گرفته‌اند که نباید گنگ و گرد سخن بگویند. دارند دنبال گردی‌های سخن خود می‌گردند. تا اینجا هم اگر استدلالشان گویاتر شده، به کمک مثال‌های من بوده است. ولی دارند آماده می‌شوند تا نسخه‌ی به‌تری از استدلالشان را رو کنند. امّا خواهش می‌کنم که سخن آخرم را به دل نگیرند و بشنوند و بیندیشند. مرتضی و بهرام عزیز، استدلال شما هنوز هیچ چیزی بیش‌تر از صورت مساله در خود ندارد. پیش‌تر این را هم نداشت.

... بسیار ادامه دارد