بررسی رفتار تابع e^x

در این جا بر آن نیستیم که چیزی را ثابت کنیم. در هر کتاب مقدّماتی دیفرانسیل به سادگی اثبات این گزاره دیده می‌شود که: ‎ $(e^x)'$ = e^x‎
ولی دیدن این برابری خالی از لطف نیست.

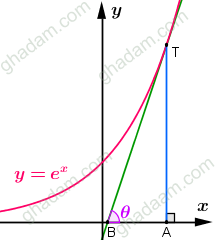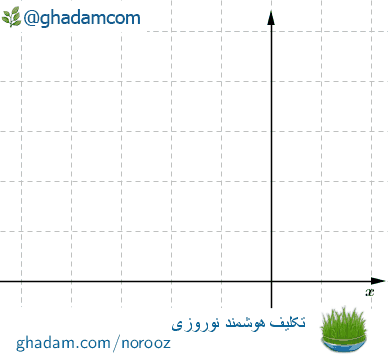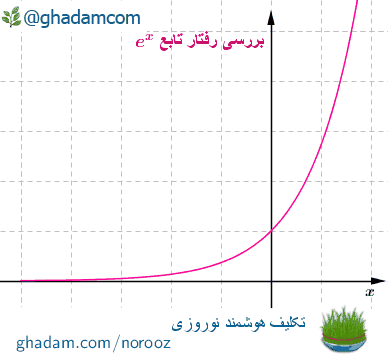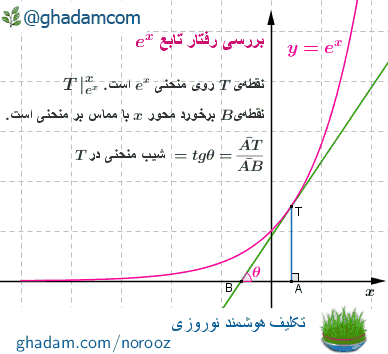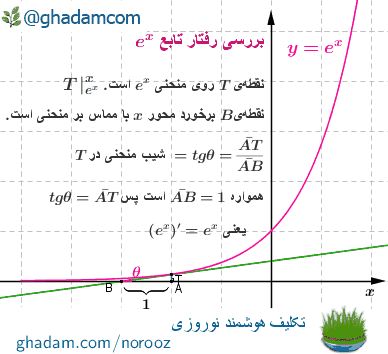
تکلیف آنلاین، حسابان، دیفرانسل، مشتق، تابع نمایی در نقطه‌ی $T$ از منحنی، مماسی بر این منحنی می‌کشیم. این مماس با محور x در B برخورد می‌کند. تصویر T بر محور $x$ را نیز A می‌گیریم.

چنان که می‌دانید، شیب منحنی ‎e^x‎ در نقطه‌ی $T$ همان $tg \hspace{3}T\hat{B}A = tg \theta$ است. پس داریم:

tg θ = $\frac{\bar{AT}}{\bar{BT}}$

مقدار تابع ‎e^x‎ در نقطه‌ی A برابر $\bar{AT}$ است. این مقدار چنان که ثابت شده است، برابر مقدار مشتق تابع ‎e^x‎ در همان نقطه نیز هست. پس باید همیشه و به ازای نقطه‌ی متغیّر A داشته باشیم: $tg \theta = \bar{AT}$
یعنی در همه‌ی حالت‌ها مقدار $\bar{BT}$ باید برابر با یک واحد باشد. اکنون ثابت بودن مقدار $\bar{BT}$ را در پویانمای زیر ببینید:

تکلیف آنلاین، حسابان، دیفرانسل، مشتق، تابع نمایی

درس:

حسابان

کپی‌رایت © 1397. تمامی حقوق محفوظ است.
بازنشر متن و راهنمایی‌های تمرین‌های پویا و مطالب آموزشی سایت در هر نشریه‌ی کاغذی یا رسانه‌ی الکترونیکی دیگر ممنوع است.
استفاده از مطالب دیگر سایت، با ذکر منبع بلامانع است.

«تمامی كالاها و خدمات این فروشگاه، حسب مورد دارای مجوزهای لازم از مراجع مربوطه می‌باشند و فعالیت‌های این سایت تابع قوانین و مقررات جمهوری اسلامی ایران است.»

بررسی رفتار تابع e^x

نمونه تمرين پويا

پیمایش

ورود کاربر

بررسی رفتار تابع e^x

نمونه تمرين پويا

پیمایش