طول ضلع مثلث متساوی‌الاضلاع (راه 1)

از هم‌نهشتی مثلث‌های APB و AQC و متساوی‌الساقین بودن مثلث می‌توان پی برد که PQ با BC موازی است.
تصویر P بر BC را بنامید و تلاش کنید از قضیه‌ی فیثاغورس کمک بگیرید.

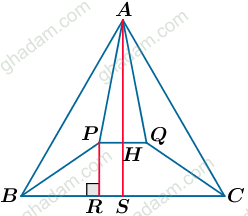
وسط PQ را H می‌نامیم.

ΔAPQ: AP = AQ , PH = QH => AH ┴ PQ   (i)    , ∠PAH = ∠QAH   (ii)

ΔAPH: AH ┴ PQ , PH = 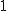=> PH² + AH² = AP² => AH² = 28 - 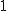= 27

از طرفی بنا بر هم‌نهشتی مثلث‌های APB و 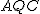برابری ‎∠CAQ = ∠BAP‎ به دست می‌آید.

از آن جا که بنا بر ii دو زاویه ی QAH و PAH نیز برابراند، درمی‌یابیم که AH نیمساز زاویه‌ی BAC است. و بنا بر قضیه‌ای بر BC عمود است.

اکنون تصویر P بر BC را R می‌گیریم. و برخورد 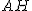با BC را نیز S می‌نامیم.
می‌توان ثابت کرد که ‎PR = SH‎ است. طبق قضیه‌ی فیثاغورس در مثلث BPR داریم:

ΔBPR : ∠BPR = 90˚ => BP² = BR² + PR² = BR² + SH²

=> 4² =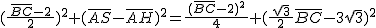

=> 64 = BC² - 4 BC + 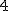+ 3 Bc² + 108 - 36 BC

=> 4 BC² - 40 BC + 48 = 0 => Bc² - 10 BC + 12 = 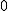=> (Bc - 5)² - 25 + 12 = 0 => (BC - 5)² - 13 = 0

=> (BC - 5 + 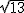) (Bc - 5 - 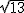) = 0

=> ‎BC = 5 + ‎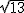     یا     ‎Bc = 5 - ‎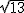

AH باید کم‌تر از 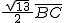باشد، پس ‎BC = 5 - √13‎ درست نیست.