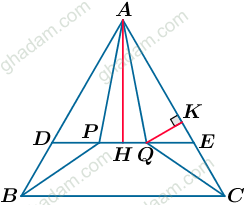
 ار همنهشتی مثلثهای ABP و ACQ میتوان نشان داد که نیمساز (یا همان ارتفاع) مثلث APQ نیمساز زاویهی
ار همنهشتی مثلثهای ABP و ACQ میتوان نشان داد که نیمساز (یا همان ارتفاع) مثلث APQ نیمساز زاویهی 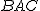 نیز هست.
نیز هست.
وسط PQ را 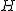 میگیریم. با کمک قضیهی فیثاغورس در مثلث AHQ داریم:
میگیریم. با کمک قضیهی فیثاغورس در مثلث AHQ داریم:
ΔAHQ : AH ┴ PQ => AQ2 = AH2 + HQ2
AH2 = 28 - 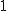 = 27 (i)
= 27 (i)
اکنون برخورد امتداد PQ با AB را به ترتیب 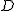 و E مینامیم.
و E مینامیم.
روشن است که ∠HAE = 30˚ است. پس بنا بر قضیهای داریم: AE = 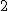 HE
HE
بنا بر قضیهی فیثاغورس در مثلث AHE داریم:
ΔAHE : ∠AHE = 90˚ => AH2 + HE2 = AE2 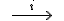 27 + HE2 = 4 HE2
27 + HE2 = 4 HE2
=> 27 = 3 HE2 => HE = 3 , HQ = 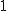 => QE = 2 (ii)
=> QE = 2 (ii)
اکنون تصویر Q بر AC را K مینامیم. در مثلث قائمالزاویهی QKE اندازهی زاویهی EQK برابر 30 درجه است. و بنا بر قضیهای داریم:
EK = 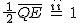
بنا بر قضیهی فیثاغورس در مثلثهای QKE و KQC داریم:
ΔQKE : ∠QKE = 90˚ => QE2 = QK2 + KE2 => QK2 = 4 - 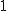 = 3 (iii)
= 3 (iii)
ΔKQC : ∠QKC = 90˚ => QC2 = QK2 + KC2 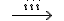 KC2 = 16 -
KC2 = 16 - 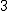 = 13 => KC = √13
= 13 => KC = √13
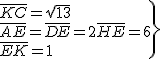 => AC = AE + KC - KE = 6 + √13 - 1
=> AC = AE + KC - KE = 6 + √13 - 1
=> AC = 5 + √13


