12 وجهی منتظم

امروز می‌خواهیم به شما یاد بدهیم که یک 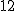وجهی منتظم برای خود درست کنید.
به آن نگاه کنید. چشم خود را ببندید و تجسم کنید و درک هندسی خود را افزایش دهید. همین.

هر یک از وجه‌های این 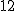وجهی منتظم، یک 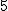ضلعی منتظم است. یعنی یک 5 ضلعی که همه‌ی ضلع‌های آن یکسان و نیز همه‌ی زاویه‌های آن یکسان باشند.
به سادگی می‌توان اندازه‌ی زاویه‌های این 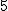ضلعی را پیدا کرد:

مجموع زاویه‌های درونی پنج‌ ضلعی ‎= (5-2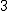)×180˚ = ×180˚‎

و چون هر 5 زاویه باید با هم برابر باشند، داریم:

اندازه‌ی هر یک از زاویه‌های پنج ‌ضلعی منتظم ‎= = 108˚

پس یک پنج‌ ضلعی منتظم این شکلی خواهد بود:

اکنون کمی تجسم کنید. بیندیشید که 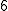تا از این 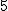ضلعی‌های منتظم دارید که همگی یکسان‌اند. حالا فکر کنید که به هر یک از ضلع‌های پنج ‌ضلعی منتظم شکل الف، یک پنج ‌ضلعی منتظم دیگر (یکسان با همان پنج‌ ضلعی شکل الف) چسبیده است.
خوب بیندیشید. آیا 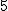تا پنج ‌ضلعی منتظمی که دور شکل الف تجسم کردید، با هم اشتراکی دارند؟ آیا ضلع‌های آن‌ها به هم چسبیده‌اند. یا نه؟

خب، اکنون جلوتر می‌رویم. اگر شکل بالا را روی کاغذ بکشید و 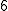پنج‌ ضلعی منتظم را یک به صورت یک تکه با قیچی ببُرید، آیا می‌توانید چیزی شبیه یک کاسه (نیم‌کره) با آن بسازید؟
بله شدنی است. هر پنج‌ضلعی کناری با 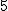ضلعی مرکزی یک لبه‌ی مشترک دارد (با خط‌چین مشخص شده است). باید کاغذ را از این لبه‌ها تا بزنید.
اما هنگامی که تا زدید، پنج ‌ضلعی کناری چه‌قدر بالا می‌آید؟

تو پای به راه در نه و هیچ مپرس خود راه بگویدت که چون باید رفت

اگر همه‌ی 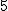تا 5 ضلعی کناری را (به کمک تا زدن لبه‌ی خط‌چین شده) بالا بیاورید، لبه‌های کناری خود این پنج ‌ضلعی‌ها به هم چفت می‌شوند. پس چیزی شبیه یک کاسه ساخته‌اید.

بخش پایانی کار بسیار گیراتر است. بیندیشید 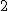تا از این کاسه‌ها ساخته‌اید. تجسم کنید که آیا شدنی است که این دو کاسه را به هم چفت و جفت کنید تا چیزی شبیه به یک توپ کم و بیش گرد بسازید؟

بله شدنی است. آن چه به دست می‌آید، یک دوازده وجهی منتظم است.

شاید روزی دلبسته‌ی مطالعه‌ی دستورهای هندسی و مساله‌های ترکیبیاتی طرح شده در این چندوجهی بشوید.