عکس قضیه
 حمید میدانست که در مثلث
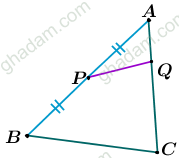
حمید میدانست که در مثلث ، پارهخط PQ نصف طول ضلع BC است و P وسط ضلع AB است. پس به یاد قضیهی میانخط افتاد.
قضیهی میانخط
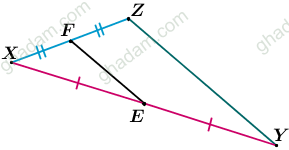 اگر E و F به ترتیب وسطهای ضلعهای XY و XZ از مثلث XYZ باشند، آنگاه
اگر E و F به ترتیب وسطهای ضلعهای XY و XZ از مثلث XYZ باشند، آنگاه با YZ موازی است و
است.
در این جا حمید نتیجه گرفت که Q نیز باید وسط ضلع AC باشد و باید موازی با BC باشد. اما او کمی احتیاط کرد. به یاد عکس قضیهی میانخط افتاد.
عکس قضیهی میانخط
اگر از وسط یکی از ضلعهای مثلث، خطی موازی با ضلع دوم مثلث کشیده شود، این خط از وسط ضلع سوم مثلث خواهد گذشت و ضلع اول و سوم مثلث، پارهخطی به طول نصف ضلع دوم مثلث بر روی خط موازی کشیده شده جدا خواهند کرد.
حمید دید که نتیجهگیری او با عکس قضیهی میانخط نیز سازگار است و این قضیه نیز استدلال او را تایید میکند.
 اما حمید اشتباه کرد. استدلال او درست نیست.
اما حمید اشتباه کرد. استدلال او درست نیست.
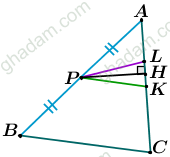
وسط ضلع را P بنامید. تصویر P بر AC را
بگیرید و وسط ضلع AC را نیز K بنامید. اکنون L را چنان بر ضلع AC بگیرید که LH=
باشد.
روشن است که مثلث PHL متساویالساقین است (چرا؟) و PK=PL است.
اگر نتیجهگیری حمید را درست بگیریم، هم K و هم L باید هر دو وسط ضلع AC باشند!
حمید اشتباه بزرگی کرده است. او در کمک گرفتن از قضیهها دچار لغزش شده است.
قضیهی میانخط به شما اطمینان می دهد که اگر وسطهای دو ضلع مثلثی را به هم وصل کنید، پارهخط به دست آمده با ضلع سوم موازی است و نصف آن طول دارد. همین، بی کم و کاست.

- فرض قضیهی میانخط: E و
وسطهای دو ضلع XY و XZ هستند.
- حکم قضیهی میانخط:
با YZ موازی است و EF=
XY است.
تنها هنگامی میتوان از قضیهی میانخط کمک گرفت که فرضهای قضیهی میانخط را داشته باشیم. (حمید همهی این فرضها را نداشت.) اگر فرضهای قضیهای را نداشته باشیم، آن قضیه کمکی به ما نمیکند. خاموش میماند. در این هنگام نه به درستیِ حکم قضیه میتوان پافشاری کرد و نه به نادرستی آن.
شاید حمید چنین فکر کرده بود که "حکم قضیهی میانخط را دارم () پس باید فرض آن را نیز داشته باشم تا حکم درست از آب دربیاید."
این فکر حمید نیز لغزش است. او یک جملهی شرطی را با عکس جملهی شرطی اشتباه گرفته است. به قول ریاضیدانها با
همارز (یعنی همارزش) نیست.
شاید این داستان به شما کمک کند. قدیمها کبریت نبود. خیلی کم بود. وقتی در خانهای آتش خاموش میشد، از همسایه آتش روشن میگرفتند.
آتش از خانهی همسایهی درویش مخواه کان چه از روزن او میگذرد دود دل است
ادامه دارد...


