نسبتهای مثلثاتی کمان دو برابر با کاغذ و تا
 به کمک یکی دو بار تا کردن کاغذ میتوانیم این دو اتحاد را ببینیم.
به کمک یکی دو بار تا کردن کاغذ میتوانیم این دو اتحاد را ببینیم.
Sin 2θ = Sinθ Cosθ
Cos 2θ = Cos2θ - 1
 یک کاغذ مستطیل شکل را از روی قطر نصف کنید تا مثلث قائمالزاویهی
یک کاغذ مستطیل شکل را از روی قطر نصف کنید تا مثلث قائمالزاویهی را به دست آورید.
گیریم که اندازهی زاویهی ACB برابر باشد.
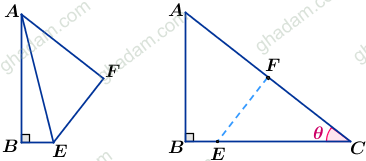 اکنون راس C را روی راس
اکنون راس C را روی راس بگذارید و کاغذ را تا کنید. سپس دوباره کاغذ را باز کنید. باید چنین شکلی بسازید:
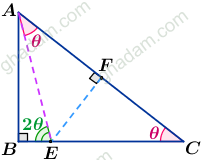 این بار کاغذ را از روی خط AE تا کنید. و باز کنید تا چنین شکلی بسازید.
این بار کاغذ را از روی خط AE تا کنید. و باز کنید تا چنین شکلی بسازید.
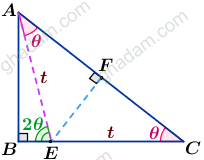 به سادگی میتوانیم طول EA =
به سادگی میتوانیم طول EA = را یک واحد بگیریم. اگر خوشتان نمیآید طول آن را برابر t میگیریم: EA=EC=t
اکنون در مثلث ABC داریم:
Sin ∠ACB = Sin θ =
-> Sin θ = -> Sin 2θ = 2 Sin θ Cos θ
از طرفی برای پیدا کردن Cos 2θ داریم:
COS ∠ACB = Cos θ =
-> Cos θ = -> Cos 2θ = 2 Cos2θ - 1


