اثبات متساوی‌الساقین بودن مثلث - راه 5

در مثلث $ABC$ اندازه‌ی دو زاویه‌ی ABC و ACB برابر است. ثابت کنید این مثلث در راس $A$ متساوی‌الساقین است.

می‌خواهم راهنمایی را ببینم.

روی ضلع $BC$ نقطه‌ی P را چنان بگیرید که ‎AP = AC‎ باشد.

می‌خواهم پاسخ را ببینم.

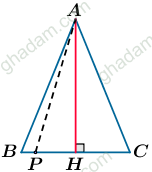
فرض: ‎C ∉ AB‎ , ‎∠ABC = ∠ACB (I)‎

حکم: ‎AB = AC‎

حل به روش برهان خلف

روشن است که پای عمود کشیده شده از A بر BC نمی‌تواند B یا 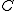$C$ باشد. زیرا در این صورت هر دو زاویه‌ی B و C برابر قائمه خواهند بود. که بنا بر قضیه‌ای درست نیست.
پس پای عمود کشیده شده از A بر BC را نقطه‌ی 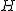$H$ می‌نامیم و فرض می‌کنیم که H وسط BC نباشد. پس قرینه‌ی C نسبت به H را P (متمایز از 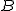$B$ ) می‌نامیم. ‎(II)‎

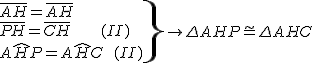$\left. \bar{AH}=\bar{AH} \\\bar{PH}=\bar{CH}\hspace{28}(II)\\A\hat{H}P=A\hat{H}C \hspace{8}(II) \right\}\to \Delta AHP =\limits^{\sim} \Delta AHC$ (به حالت ض‌زض)

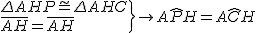$\left. \Delta AHP =\limits^{\sim} \Delta AHC\\\bar{AH}=\bar{AH} \right\} \to A\hat{P}H=A\hat{C}H$ اجزای نظیر دو مثلث

$\left. A\hat{P}H=A\hat{C}H\\A\hat{B}H=A\hat{C}H \hspace{8}(I)\right\}\to A\hat{P}H=A\hat{B}P\hspace{28}(III)$

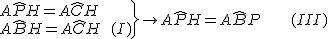
ΔABP: H ∈ BP _^قضیه__{_>} ∠APH > ∠ABP (IV)

ولی III و IV نمی‌توانند با هم درست باشند. پس به تناقض رسیده‌ایم.
پس فرض خلف درست نیست. و H نمی‌تواند وسط BC نباشد. از طرفی به دلیلی مشابه، نقطه‌ی P در امتداد BC نیز نمی‌تواند باشد. پس به هر حال 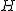$H$ وسط BC است.
و بنا بر قضیه‌ای مثلث ABC در راس A متساوی‌الساقین است.
حکم ثابت شد.

راه‌های دیگر حل این مساله را این جا ببینید. این نوع تمرین‌ها همراه با یک راهنمایی و شرحی کوتاه از راه حل هستند.

درس:

نهم- ریاضی- فصل3- استدلال و اثبات در هندسه

کپی‌رایت © 1397. تمامی حقوق محفوظ است.
بازنشر متن و راهنمایی‌های تمرین‌های پویا و مطالب آموزشی سایت در هر نشریه‌ی کاغذی یا رسانه‌ی الکترونیکی دیگر ممنوع است.
استفاده از مطالب دیگر سایت، با ذکر منبع بلامانع است.

«تمامی كالاها و خدمات این فروشگاه، حسب مورد دارای مجوزهای لازم از مراجع مربوطه می‌باشند و فعالیت‌های این سایت تابع قوانین و مقررات جمهوری اسلامی ایران است.»

اثبات متساوی‌الساقین بودن مثلث - راه 5

نمونه تمرين پويا

پیمایش

ورود کاربر

اثبات متساوی‌الساقین بودن مثلث - راه 5

نمونه تمرين پويا

پیمایش