داستان های استدلال - مجموع زاویه های درونی مثلث (بخش 1)

پیش از این که بخواهیم تمرین‌های هفته را حل کنیم‏، باران دستش را بالا برد.

باران: خانم یادم هست که مانند کتاب اشاره کرده بودید که مجموع زاویه‌های درونی مثلّث برابر ‎180˚‎ است و یادآوری کردید که این قضیه اثبات می‌شود و دلیل دارد. ولی در کتاب بدون اثبات آمده است.

من از دانش‌آموزان پارسال، همه‌ی تمرین‌ها و آزمون‌های شما را گرفتم. در یکی از آن‌ها راهنمایی کرده بودید تا اثبات را پیدا کنند. من پیدا کردم، اجازه می دهید بگویم؟

من: خیلی خوب است. بیا و روی تخته هر چه می‌خواهی بنویس و بگو.

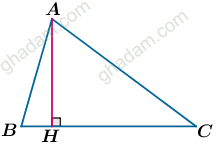
باران: من کمی راه را تغییر دادم. در مثلّث از راس A، ارتفاع AH را می‌کشیم. تا دو مثلّث ABH و ساخته شوند. حالا به مجموع زاویه‌های هر سه مثلّث ABC، و ACH توجه می‌کنیم.

همین جا نفیسه اعتراض داشت که با اشاره‌ی من خاموش شد.

باران نوشت:

ABC مجموع زاویه‌های مثلّث ‎ = ∠BAC + ∠ABC + ∠BCA‎
مجموع زاویه‌های مثلّث ‎ = ∠BAH + ∠ABH + ∠BHA‎
مجموع زاویه‌های مثلّث ‎ = ∠CAH + ∠ACH + ∠CHA‎

حالا مجموع زاویه‌های مثلّث را برابر می‌گیریم و دو برابری آخر را با هم جمع می‌کنیم:

x = ∠BAH + ∠CAH + ∠ABH + ∠ACH + ∠BHA + ∠CHA

همین جا لیلا و اعظم اجازه خواستند که چیزی بگویند. کمی هم مردد بودند و نگاهشان تخته را مرور می‌کرد. اما من از آن‌ها خواستم که اجازه بدهند باران حرفش را تمام کند.

باران:‌ در آخرین برابری مقدار ‎90˚‎ را جاگذاری می‌کنیم و بعضی زاویه‌ها را دوباره نام‌گذاری می‌کنیم.
و توجه می‌کنیم که ‎∠BAH + ∠CAH =‎ است:

x = ∠BAC + ∠ABC + ∠ACB + 90˚ + 90˚

اما ‎∠BAC + ∠ABC + ∠ACB‎ همان مجموع زاویه‌های درونی مثلّث، یعنی است. پس داریم:

x = x + 180˚ => x - x = 180˚ => = 180˚

پس مجموع زاویه‌های درونی مثلّث برابر ‎180˚‎ است.

از بچه‌ها خواستم که به استدلال باران فکر کنند. الان دو سه نفر دیگر هم می‌خواستند حرف بزنند.

ادامه دارد ....

بخش‌های بعدی این داستان:

• بخش 2
• بخش 3
• بخش 4