تشخیص تابع نمایی از روی شکل منحنی

صفحه‌ی 95 و 96 کتاب درسی ریاضی 2 در پرسشی از دانش‌آموزان می‌خواهد که تابع نمایی را از روی رفتار نمودار هندسی تغییرات آن بشناسند.

تکلیف آنلاین، آموزش ریاضی، تابع نمایی، ریاضی2

برخی از ویژگی‌های تابع نمایی بی‌درنگ به چشم می‌ایند. شاید برجسته‌ترینِ این ویژگی‌ها متقارن نبودن تابع نمایی باشد. مجانب افقی این منحنی و شاخه‌ی بینهایت آن از همین ویژگی‌های برجسته هستند.
گذشته از این برجستگی ها پرسشی هست که همواره دانش‌آموزان کنجکاو را مشغول می‌کند:

اگر تنها بخشی از منحنی نمودار تغییرات تابع نمایی را داشته باشیم، چه کنیم؟
گویی چشم تفاوتی بین برخی تکه‌های سهمی و منحنی تابع نمایی نمی‌بیند.

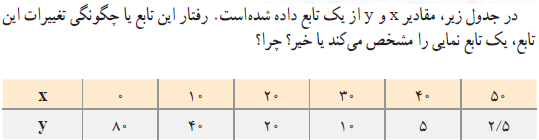
کتاب درسی ریاضی 2، در صفحه‌ی 94 برای شناخت تابع نمایی از روی مقدارهای مختلف تابع نمونه‌ای آورده است که بسیار راه‌گشا است.

تکلیف آنلاین، آموزش ریاضی، تابع نمایی، ریاضی2

کار خودمان را از همین جا آغاز می‌کنیم.‎a^(x+t) = $a^x$ × a^t‎

برای مقدار تابع در دو نقطه با طول‌های x و ‎x+ $t$ ‎ داریم: ‎f(x+t) = a^x+t = $a^x$ ×a^t = a^t f(x)‎

یعنی رشد $x$ به اندازه‌ی t، مقدار تابع را از ‎f(x)‎ به ‎a^t f(x)‎ تغییر می‌دهد.
این ویژگی شاید با چشم به خوبی دیده نشود. برای چاره کمی هندسه چاشنی کار می‌کنیم:

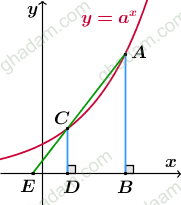تکلیف آنلاین، آموزش ریاضی، تابع نمایی، ریاضی2 چنان که گفتیم ‎AB = a^t . CD‎ و از طرفی برخورد $CD$ با محور x را $E$ می‌نامیم و به تشابه دو مثلث ABE و CDE می‌پردازیم:

${{\hspace{2}\bar{DE}\hspace{2}}\over{\bar{BE}}}={{\hspace{2}\bar{CD}\hspace{2}}\over{\bar{AB}}}={{\hspace{2}\bar{CD}\hspace{2}}\over{a^t.\bar{CD}}}={{\hspace{2}1\hspace{2}}\over{a^t}} \to {{\hspace{2}\bar{DE}\hspace{2}}\over{\bar{BE}}}={{\hspace{2}1\hspace{2}}\over{a^t}}$

$\to {{\hspace{2}\bar{DE}\hspace{2}}\over{\bar{BE}-\bar{DE}}} ={{\hspace{2}1\hspace{2}}\over{a^t-1}}$ -> DE = ${{\hspace{2}1\hspace{2}}\over{a^t-1}}$

(در حالتی که تابع ‎a^x‎ روند کاهشی داشته باشد، محاسبات کمی تغییر می‌کند ولی نتیجه مشابه است.)
یعنی DE طولی ثابت دارد. که در تابع‌های دیگر چنین نیست.

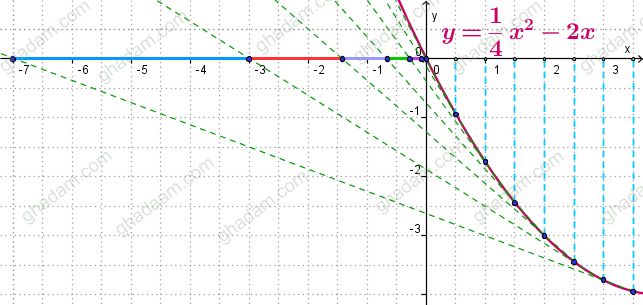
در شکل پایین سهمی ‎y = ${{\hspace{2}1\hspace{2}}\over{4}}$ x² - 2 x‎ را می‌بینید. خط‌های آبی عمود بر محور x و با فاصله‌ی 0.5 واحد از یکدیگر کشیده شده‌اند.
چنان که می‌بینید با تغییر x، طول پاره‌خط DE ثابت نمی‌ماند و تغییر می‌کند.

البتّه برای شلوغ نشدن شکل، پاره خط‌های DE رنگ نشده‌اند. پاره خط‌های رنگی شکل فاصله‌ی بین E های مختلف هستند.

تکلیف آنلاین، آموزش ریاضی، تابع نمایی، ریاضی2

در شکل زیر همان کار را با تابع نمایی ‎2^x‎ انجام داده‌ایم.
چنان که می‌بینید پاره‌خط‌های DE روی محور x ساخته شده‌اند و همگی طول برابر دارند.

البتّه برای شلوغ نشدن شکل، پاره خط‌های DE رنگ نشده‌اند. پاره خط‌های رنگی شکل فاصله‌ی بین E های مختلف هستند.

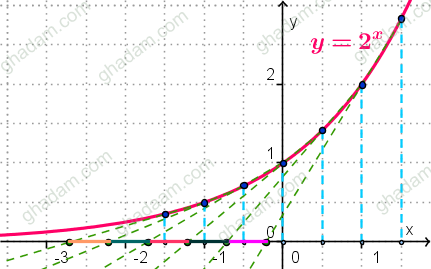
تکلیف آنلاین، آموزش ریاضی، تابع نمایی، ریاضی2

هم‌چنین اگر دو نقطه‌ی $A$ و C از منحنی را بسیار به هم نزدیک کنیم تا رفتار حدی تابع را بررسی و مشاهده کنیم، تماشایی خواهد بود.
می‌توانید این جا را تماشا کنید.

اما کشیدن مماس بر منحنی و بررسی رفتار منحنی به کمک آن دو محدودیت دارد.

دانش‌آموزان پایه‌های پاین‌تر با مفهوم مشتق و شیب منحنی آشنا نیستند.
کشیدن مماس بر منحنی (منحنی نامشخص) کار ساده‌ای نیست.

از این رو بر آن شدم که شیب وترهای منحنی را بررسی کنم و نتیجه همین نوشته شد.

درس:

دهم- رياضي1

نمونه تمرين پويا

تشخیص تابع نمایی از روی شکل منحنی

پیمایش

ورود کاربر

نمونه تمرين پويا

تشخیص تابع نمایی از روی شکل منحنی

پیمایش